D. graph and its complement

Author: aulr

August undefined, 2024

WebGraphDifference gives the graph obtained from the union of vertex sets of two graphs and the complement of the second graph ’ s edge set with respect to the first. GraphComplement gives the graph that has the same vertex set as a given graph, but with edges corresponding to absent edges in the original (and vice versa). WebJan 1, 2013 · The Kirchhoff index is the sum of resistance distances between all pairs of vertices in G. Zhou and Trinajstić (Chem Phys Lett 455(1–3):120–123, 2008) obtained a Nordhaus-Gaddum-type result ...

Complement of Graph in Graph Theory Example

WebThe energy of the graph had its genesis in 1978. It is the sum of absolute values of its eigenvalues. It originates from the π -electron energy in the Huckel molecular orbital model but has also gained purely mathematical interest. ... T1 - Laplacian energy of partial complement of a graph. AU - D'Souza, Sabitha. AU - Nayak, Swati. AU - Bhat ... Webgraph and its complement are known as Nordhaus-Gaddum inequal-ities. In this paper, some variations on this result is studies. First, recall their theorem, which gives bounds on the sum and the product of the chromatic number of a graph with that of its complement. we also provide a new characterization of the certain graph classes. orcl数据库安装

Algebraic connectivity of the second power of a graph - Afshari ...

Web2.5K views 2 years ago What is the complement of a complete bipartite graph? Recall that a bipartite graph is a graph whose vertices can be partitioned into two partite sets, say … WebFeb 1, 2024 · A subgraph complement of the graph G is a graph obtained from G by complementing all the edges in one of its induced subgraphs. We study the following algorithmic question: for a given graph G and graph class $${\\mathscr {G}}$$ G, is there a subgraph complement of G which is in $${\\mathscr {G}}$$ G? We show that this … WebApr 10, 2024 · Shareable Link. Use the link below to share a full-text version of this article with your friends and colleagues. Learn more. iracing refresh rate

Basic Properties of a Graph - GeeksforGeeks

Complement of Graph in Discrete mathematics - javatpoint

WebA: Lagrange multiplier: For Part (a) In mathematical optimization, the method of Lagrange multipliers…. Q: Prove that the following claim holds when for all n ≥1 n (n+1) (n+2) 71 Σ (i²+i)= 3 i=1. A: Click to see the answer. Q: 1) R is as Set D Shown double mass that occupres, point up the for the total lamina if any from the…. Web(c)Find a simple graph with 5 vertices that is isomorphic to its own complement. (Start with: how many edges must it have?) Solution: Since there are 10 possible edges, Gmust have 5 edges. One example that will work is C 5: G= ˘=G = Exercise 31. (a)Draw the isomorphism classes of connected graphs on 4 vertices, and give the vertex and edge iracing refund membershipWebDec 1, 1998 · Let G = (V,E) be a graph on n vertices. Denote by d(v) the degree of v ∈ V and by m(v) the average of the degrees of the vertices of G adjacent to v.Then b(G) = max{m(v) + d(v): v ∈ V} is an upper bound for the Laplacian spectral radius of G; hence, n − b(G C) is a lower bound for the algebraic connectivity of G in terms of the vertex degrees … orcl数据库备份语句

"WebThe number of vertices in graph G equals to the number of vertices in its complement graph G1`. The symbolic representation of this relation is described as follows: 2. The … " - D. graph and its complement

D. graph and its complement

Relationship between Coloring a graph and its complement

WebJun 1, 1980 · Both a graph and its complement are self-centered with identical radius Article Full-text available Jan 2024 Chellaram Malaravan Arumugam View Show abstract ... Theorem A. For a graph G... The fact that the complement of a perfect graph is also perfect is the perfect graph theorem of László Lovász. Cographs are defined as the graphs that can be built up from single vertices by disjoint union and complementation operations. They form a self-complementary family of graphs: the complement of any … See more In the mathematical field of graph theory, the complement or inverse of a graph G is a graph H on the same vertices such that two distinct vertices of H are adjacent if and only if they are not adjacent in G. That is, to generate the … See more Several graph-theoretic concepts are related to each other via complementation: • The complement of an edgeless graph is a complete graph and vice versa. • Any induced subgraph of the complement graph of a graph G is the complement of the corresponding … See more In the analysis of algorithms on graphs, the distinction between a graph and its complement is an important one, because a See more Let G = (V, E) be a simple graph and let K consist of all 2-element subsets of V. Then H = (V, K \ E) is the complement of G, where K \ E is the See more A self-complementary graph is a graph that is isomorphic to its own complement. Examples include the four-vertex path graph and … See more

Did you know?

Webwith any of the original graphs. The graph C 5 is its own complement (again see Problem 6). We now examine C n when n 6. The graph C n is 2-regular. Therefore C n is (n 3)-regular. Now, the graph N n is 0-regular and the graphs P n and C n are not regular at all. So no matches so far. The only complete graph with the same number of vertices as ... WebThen think about its complement, if two vertices were in different connected component in the original graph, then they are adjacent in the complement; if two vertices were in the …

WebComplement of Graph in Graph Theory- Complement of a graph G is a graph G' with all the vertices of G in which there is an edge between two vertices v and w if and only if there exist no edge between v and w in the … Webwith any of the original graphs. The graph C 5 is its own complement (again see Problem 6). We now examine C n when n 6. The graph C n is 2-regular. Therefore C n is (n 3) …

WebJun 15, 2024 · On Energy and Laplacian Energy of Graphs. K. Das, Seyed Ahmad Mojalal. Mathematics. 2016. Let G = (V,E) be a simple graph of order n with m edges. The energy of a graph G, denoted by E (G), is defined as the sum of the absolute values of all eigenvalues of G. The Laplacian energy of the…. Expand. Web2 and how well-connected the graph is, the symmetric formulation of the Laplacian spread conjecture in (3) can be interpreted as stating that a graph and its complement cannot both be very poorly connected. ∗Department of Mathematics, Brigham Young University, Provo, UT, [email protected]

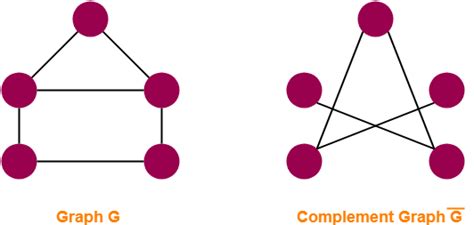
WebAug 23, 2024 · In the following example, graph-I has two edges 'cd' and 'bd'. Its complement graph-II has four edges. Note that the edges in graph-I are not present in …

WebMar 24, 2024 · A maximally nonhamiltonian graph is a nonhamiltonian graph G for which G+e is Hamiltonian for each edge e in the graph complement of G^_, i.e., every two nonadjacent vertices are endpoints of a Hamiltonian path. Since an edge added between two disconnected components of a disconnected graphs is a bridge, and after crossing a … iracing renewal discount 2023WebTranscript. Changes in the prices of related products (either substitutes or complements) can affect the demand curve for a particular product.The example of an ebook illustrates how the demand curve can shift to the … orcmbWebWe know that for any graph G the independence number D(G) is always equal to the clique number of its complement Z(G), i.e., If Z(G) is the clique number of the graph G and D(G) is the independence number of its complement G the we have, Z(G) D(G). Therefore F(G) D(G). Proposition 2.4 For any Graph G if G is Berge then F(G) D(G). orcl数据库备份WebCOMPLEMENTARY GRAPHS AND TOTAL CHROMATIC NUMBERS* ROGER J. COOKt Abstract. A theorem of the Nordhaus-Gaddum class is obtained for the total chromatic number of a graph and its complement. The complement G of a graph G is the graph with the same vertex set as G and in which two vertices are adjacent if and only if they … orcmeetingsWebTherefore, either the simple graph G or its complement graph G C, must be connected. QED. 9. In a connected graph, the distance d(v,w) between a vertex v and a vertex w is the length of the shortest path from v to w. (i) If d(v,w) >= 2, show that there exists a vertex z such that d(v,z)+d(z,w)=d(v,w). iracing renew subscription on steamWebits focus is on ﬁnite graphs. Therefore all graphs will be ﬁnite, unless otherwise stated. Exceptions are Sections 3.6, 3.7, and 3.11, where graphs are generally inﬁnite, and Sections ... We start with the simplest examples. A graph and its complement have the same automorphisms. The automorphism group of the complete graph Kn and the empty orcna ca websiteWebApr 7, 2024 · The graph thus obtained is called δ-complement of G. For any two points u and v of G with degu≠degv remove the lines between u and v in G and add the lines between u and v that are not in G. iracing replay cameras